Join Us On Social Media!
Italy
Recent Posts
📝 Question of the Day?
8 hours ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 16 Views · 0 Likes
Flag
📝 Reply
Hi Ross, I completely agree with you.
Without offense or criticism, because everyone is free to think as they wish, I think this is a very interesting topic and absolutely consistent with this site and with naval modeling.
I like knowing the name and function of each element that makes up a hull, the rigging and the sails.
I know them very well because it's a fun topic for me, and now, thanks in part to this site, I'm even learning the English terms.
Without offense or criticism, because everyone is free to think as they wish, I think this is a very interesting topic and absolutely consistent with this site and with naval modeling.
I like knowing the name and function of each element that makes up a hull, the rigging and the sails.
I know them very well because it's a fun topic for me, and now, thanks in part to this site, I'm even learning the English terms.
▲
⟩⟩
No likes yet
This member will receive 1 point
for every like received
This member will receive 1 point
for every like received
Login To
Remove Ads
Remove Ads
💬 Re: Business end
1 day ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 16 Views · 2 Likes
Flag
💬 Add Comment
Follow your aesthetic taste, Jumpugly, you do very well.
I'm not a big fan of super-fast boats, but I have to say that your construction is fascinating and intriguing me precisely because of the way you describe it.
The construction phases are very interesting.
I'm not a big fan of super-fast boats, but I have to say that your construction is fascinating and intriguing me precisely because of the way you describe it.
The construction phases are very interesting.
▲
⟩⟩
hermank
jumpugly
💬 Re: Business end
1 day ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 18 Views · 2 Likes
Flag
💬 Add Comment
Hi Jumpugly, it has to please and satisfy you, so it's fine.
I can't quite see the extent and effect of the change; the difference must be very small, or the photo doesn't quite capture the reality.
Is it a slightly lighter shade than the previous one?
I can't quite see the extent and effect of the change; the difference must be very small, or the photo doesn't quite capture the reality.
Is it a slightly lighter shade than the previous one?
▲
⟩⟩
hermank
jumpugly
📝 Antique compass for a ship from the second half of the 18th century.
2 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 17 Views · 2 Likes
Flag
📝 Reply
Hi Ross, no, I didn't actually mean to challenge you, but now you've reminded me that your model is 1:24 scale.
Actually, to verify this, I had to reread a post of yours from about two years ago in which you described the Bluenose model, its length, and its scale.
Yes, I'm convinced that with your skills, if you wanted, you could make a compass that would be a small masterpiece.
There's just one problem: you have a very specific reference naval model, so you should look for photos and drawings of its compass. I have no idea what the Bluenose's compass looked like.
Actually, to verify this, I had to reread a post of yours from about two years ago in which you described the Bluenose model, its length, and its scale.
Yes, I'm convinced that with your skills, if you wanted, you could make a compass that would be a small masterpiece.
There's just one problem: you have a very specific reference naval model, so you should look for photos and drawings of its compass. I have no idea what the Bluenose's compass looked like.
▲
⟩⟩
hermank
SimpleSailor
📝 Antique compass for a ship from the second half of the 18th century.
3 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 20 Views · 1 Like
Flag
📝 Reply
Thanks, Chris, I agree. Wood and brass are great aesthetic elements.
If it were 1:24 scale, it would have been a beautiful, meticulously crafted piece.
If it were 1:24 scale, it would have been a beautiful, meticulously crafted piece.
▲
⟩⟩
hermank
📝 Antique compass for a ship from the second half of the 18th century.
3 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 20 Views · 1 Like
Flag
📝 Reply
Hi Phil, I'll give it a try, I hope I succeed and don't disappoint you.
With the lifeboats, I was blinded by both the hull and the details, but it was worth it.
With the lifeboats, I was blinded by both the hull and the details, but it was worth it.
▲
⟩⟩
hermank
📝 Question of the Day?
3 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 45 Views · 3 Likes
Flag
📝 Reply
I wish you a speedy recovery, EdW. When you're well, you can answer today's questions.
▲
⟩⟩
Steves-s
Nickthesteam
DuncanP
📝 Question of the Day?
3 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 45 Views · 2 Likes
Flag
📝 Reply
The topic has already been covered but the question was different.
▲
⟩⟩
Steves-s
Nickthesteam
📝 Antique compass for a ship from the second half of the 18th century.
3 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 30 Views · 3 Likes
Flag
📝 Reply
Hi Ross, I don't think I fully understood the question, sorry.
If you mean I'll create a "build blog" section just for this element, the answer is definitely no.
Just dedicate a dedicated topic on the forum.
My idea is this:
A ship model has many phases and many interesting parts.
I'll list a few just as an example:
Hull construction.
Mast construction.
Sails.
Rigging.
Propulsion.
Propeller shaft.
Waterproofing.
Painting.
Lifeboats.
Sail control system.
Lateral stability.
Buoyancy.
Other deck elements.
Some people (after seeing the finished model) might be interested in just one of these topics and be curious to understand how it was made.
For example, in a few months, or a year, or even tomorrow, someone might be interested in knowing how the lifeboats were made (which are a separate project for the hull as well).
Well, it will be very complicated and difficult to search for this single topic in the topic dedicated to building the model because it is now so vast. The slowness of the search will discourage you.
If, however, the topic of lifeboats is discussed in the forum as a separate topic, it will be very easy (even after a long time) to do a text search.
I say this because I myself searched for some old messages in the gunboat schooner topic and had a lot of trouble and time finding them.
In fact, I also recommend that you, who are building a very complex model, divide the subtopics (perhaps linking them to the main topic to maintain an overview).
If you mean I'll create a "build blog" section just for this element, the answer is definitely no.
Just dedicate a dedicated topic on the forum.
My idea is this:
A ship model has many phases and many interesting parts.
I'll list a few just as an example:
Hull construction.
Mast construction.
Sails.
Rigging.
Propulsion.
Propeller shaft.
Waterproofing.
Painting.
Lifeboats.
Sail control system.
Lateral stability.
Buoyancy.
Other deck elements.
Some people (after seeing the finished model) might be interested in just one of these topics and be curious to understand how it was made.
For example, in a few months, or a year, or even tomorrow, someone might be interested in knowing how the lifeboats were made (which are a separate project for the hull as well).
Well, it will be very complicated and difficult to search for this single topic in the topic dedicated to building the model because it is now so vast. The slowness of the search will discourage you.
If, however, the topic of lifeboats is discussed in the forum as a separate topic, it will be very easy (even after a long time) to do a text search.
I say this because I myself searched for some old messages in the gunboat schooner topic and had a lot of trouble and time finding them.
In fact, I also recommend that you, who are building a very complex model, divide the subtopics (perhaps linking them to the main topic to maintain an overview).
▲
⟩⟩
SimpleSailor
hermank
RossM
📝 Antique compass for a ship from the second half of the 18th century.
4 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 57 Views · 3 Likes
Flag
📝 Reply
Yes, Chugalone, I intend to make the compass from scratch using the photos I attached to build one as similar as possible.
I'll use wood and brass.
I don't think I could make such a piece with a 3D printer; I think it's objectively difficult to make a piece less than 2 cm tall with all that detail.
Consider that a 1.80 m tall man is 3 cm tall in scale, so the compass (which will be at stomach height) will need to be about 1.20 m, more or less.
I'll use wood and brass.
I don't think I could make such a piece with a 3D printer; I think it's objectively difficult to make a piece less than 2 cm tall with all that detail.
Consider that a 1.80 m tall man is 3 cm tall in scale, so the compass (which will be at stomach height) will need to be about 1.20 m, more or less.
▲
⟩⟩
chugalone100
Doogle
hermank
📝 Antique compass for a ship from the second half of the 18th century.
4 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 57 Views · 11 Likes
Flag
📝 Reply
Good evening everyone.
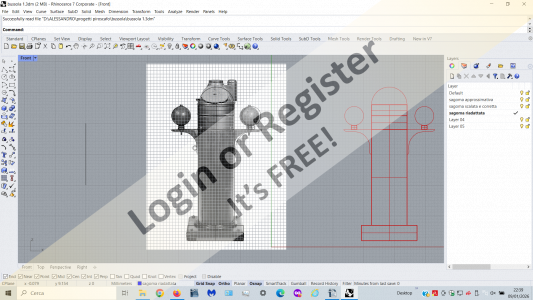
After putting it off for a long time, out of laziness, I've decided to make one of the last pieces to complete the model.
It's the compass.
With a larger scale, I could have made a beautiful, valuable piece, but at 1:60 it will probably be a bit sloppy, certainly not accurate.
I still have to make it myself because the finished piece is available, but it's a bit out of scale and I don't like it, so I hope to do better.
I'm attaching the photos I think I'll draw inspiration from.
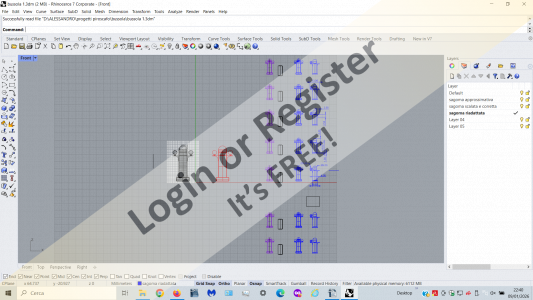
I used one of those photos to transfer it into my drawing program. This way, I can get an idea of the dimensions and proportions.
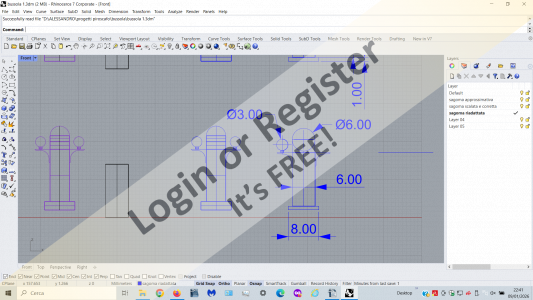
From the first drawing traced on the photo, I created another that better fits the wooden pieces I already have (cylinders and spheres).
From this, I then created the 1:60 scale model.
Now I'll have to start cutting, gluing, sanding, painting, etc.
I've decided to create a separate topic because I realized I made a mistake by describing the entire ship model in a single thread.
Now, with 548 posts, it's practically impossible to search for old posts, much less go over the entire construction process from the beginning. It's a very long and tedious job, even with very powerful computers.
At the end of this post, I'll link to the construction the compass refers to, and in that topic, I'll link to this one.
I should have done this from the beginning.








After putting it off for a long time, out of laziness, I've decided to make one of the last pieces to complete the model.
It's the compass.
With a larger scale, I could have made a beautiful, valuable piece, but at 1:60 it will probably be a bit sloppy, certainly not accurate.
I still have to make it myself because the finished piece is available, but it's a bit out of scale and I don't like it, so I hope to do better.
I'm attaching the photos I think I'll draw inspiration from.
I used one of those photos to transfer it into my drawing program. This way, I can get an idea of the dimensions and proportions.
From the first drawing traced on the photo, I created another that better fits the wooden pieces I already have (cylinders and spheres).
From this, I then created the 1:60 scale model.
Now I'll have to start cutting, gluing, sanding, painting, etc.
I've decided to create a separate topic because I realized I made a mistake by describing the entire ship model in a single thread.
Now, with 548 posts, it's practically impossible to search for old posts, much less go over the entire construction process from the beginning. It's a very long and tedious job, even with very powerful computers.
At the end of this post, I'll link to the construction the compass refers to, and in that topic, I'll link to this one.
I should have done this from the beginning.











▲
⟩⟩
premecekcz
IanL1
JockScott
Doogle
EdW
Wolle
Newby7
jumpugly
bruce1946
hermank
chugalone100
Login To
Remove Ads
Remove Ads
📝 Mary Ann 472
4 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 21 Views · 0 Likes
Flag
📝 Reply
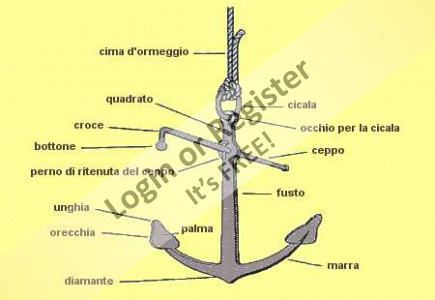
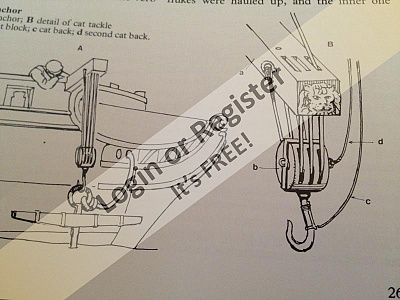
Hi Ron, as I was telling you, that type of anchor is called an admiralty anchor.
In the model preceding the one I'm finishing now, I used a much simpler solution. I used a Hall-type anchor (see photo) partially protruding from the hawsehole.
A small aside regarding translations, which we discussed privately: in Italian, it's called "occhio di cubia" (a hawsehole); well, no normal translator like Google Translate finds the correct nautical term. Google translates it as "hawse eye," which is incorrect.
This time, I know why we're using the word "occhio" (eye). In ancient times (Roman, Greek, Egyptian, and Phoenician ships), fake eyes were painted around those holes.
I couldn't do the same for the current model because it wouldn't have been consistent with the historical period.
I saw that the admiralty anchor was perfect and was actually used for those types of ships.
I could have built it myself, but since I'd already wasted a lot of time and the Amati one was very well made, I decided to buy them ready-made.
I then studied the system for placing it on board, as you can see from the photos.
Initially, I was perplexed by your choice because I thought it was an anchor used mainly on large military vessels.
Although it fell into disuse and was replaced by other, more modern types, it was very widespread and used in its time (and for a long period of time) in many fields.
I can confirm that the stock (in Italian "ceppo") was removable and secured with a cotter pin. However, I advise against placing the anchor vertically resting on the gunwale (especially without tying it down) because in reality, with the rolling and pitching movements, it would certainly fall.
It wouldn't be realistic to place an anchor resting like that, even at anchor.
An inboard anchor is fine for that type of vessel, but it would be better to place it on the deck and secure it with some ropes.
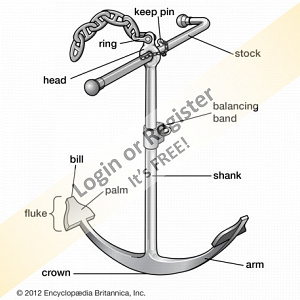
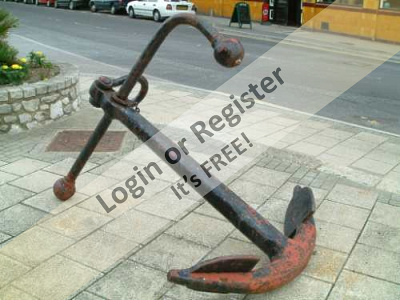




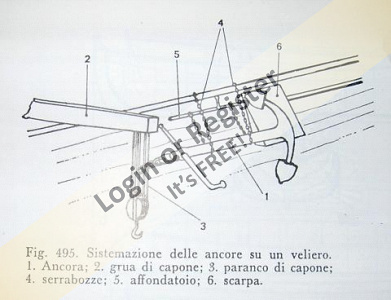

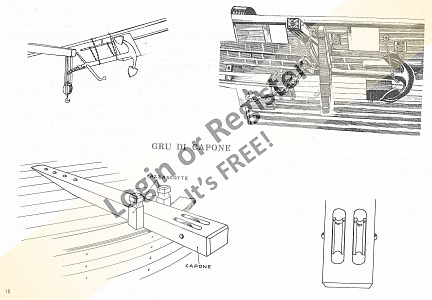

In the model preceding the one I'm finishing now, I used a much simpler solution. I used a Hall-type anchor (see photo) partially protruding from the hawsehole.
A small aside regarding translations, which we discussed privately: in Italian, it's called "occhio di cubia" (a hawsehole); well, no normal translator like Google Translate finds the correct nautical term. Google translates it as "hawse eye," which is incorrect.
This time, I know why we're using the word "occhio" (eye). In ancient times (Roman, Greek, Egyptian, and Phoenician ships), fake eyes were painted around those holes.
I couldn't do the same for the current model because it wouldn't have been consistent with the historical period.
I saw that the admiralty anchor was perfect and was actually used for those types of ships.
I could have built it myself, but since I'd already wasted a lot of time and the Amati one was very well made, I decided to buy them ready-made.
I then studied the system for placing it on board, as you can see from the photos.
Initially, I was perplexed by your choice because I thought it was an anchor used mainly on large military vessels.
Although it fell into disuse and was replaced by other, more modern types, it was very widespread and used in its time (and for a long period of time) in many fields.
I can confirm that the stock (in Italian "ceppo") was removable and secured with a cotter pin. However, I advise against placing the anchor vertically resting on the gunwale (especially without tying it down) because in reality, with the rolling and pitching movements, it would certainly fall.
It wouldn't be realistic to place an anchor resting like that, even at anchor.
An inboard anchor is fine for that type of vessel, but it would be better to place it on the deck and secure it with some ropes.


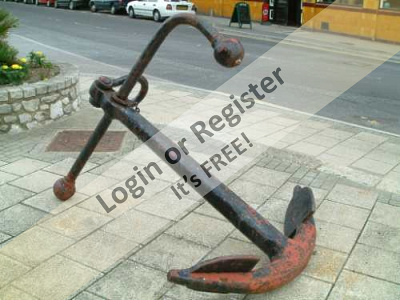









▲
⟩⟩
No likes yet
This member will receive 1 point
for every like received
This member will receive 1 point
for every like received
📝 Mary Ann 472
5 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 26 Views · 1 Like
Flag
📝 Reply
Hi Ron, sorry for writing so late, but lately I've been a bit lazy with translating posts, and the more time passes, the more messages pile up within the same topic, so I always put it off.
The topic of the anchor was very interesting to me, and I really appreciated your detailed research and, above all, your research into sources.
I don't think I need to add much because you're making a kit (if I'm not mistaken), so just follow the instructions.
I can tell you that I studied that type of anchor some time ago because it was the best one to put on my model, and at first I had some doubts.
I'll finish completing some translations and tell you mine.
I'll tell you in advance that, in my case, for that type of anchor (as you surely know, it's called an admiralty anchor), I had to study the correct way to keep it on board, the correct systems for lowering it, raising it, and securing it. They weren't at all obvious.
The topic of the anchor was very interesting to me, and I really appreciated your detailed research and, above all, your research into sources.
I don't think I need to add much because you're making a kit (if I'm not mistaken), so just follow the instructions.
I can tell you that I studied that type of anchor some time ago because it was the best one to put on my model, and at first I had some doubts.
I'll finish completing some translations and tell you mine.
I'll tell you in advance that, in my case, for that type of anchor (as you surely know, it's called an admiralty anchor), I had to study the correct way to keep it on board, the correct systems for lowering it, raising it, and securing it. They weren't at all obvious.
▲
⟩⟩
Ronald
📝 Dutch sailing barge
5 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 20 Views · 4 Likes
Flag
📝 Reply
Hi Andy, I wasn't sure I remembered correctly, so I decided to reread the previous messages.
I remembered you tried to stabilize the boat without using the protruding fin.
Is this an alternative (a plan B) or have you already noticed that it doesn't have enough capacity to right itself? Is that why you have to use the ballast under the fin?
In any case, you did a great job, but I'm very interested and fascinated by the aspects related to stability and the general physics of ships.
I remembered you tried to stabilize the boat without using the protruding fin.
Is this an alternative (a plan B) or have you already noticed that it doesn't have enough capacity to right itself? Is that why you have to use the ballast under the fin?
In any case, you did a great job, but I'm very interested and fascinated by the aspects related to stability and the general physics of ships.
▲
⟩⟩
Ronald
AndyB2
hermank
DuncanP
💬 Re: Construction report "Pilot Cutter Britannia" 1 : 24
5 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 21 Views · 4 Likes
Flag
💬 Add Comment
Good resumption of work Wolle.
▲
⟩⟩
stevedownunder
jumpugly
Wolle
hermank
📝 Question of the Day?
6 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 45 Views · 3 Likes
Flag
📝 Reply
Luckily for us, this time the three wrong options chosen by the AI were truly inconsistent.
▲
⟩⟩
Steves-s
SimpleSailor
RossM
📝 Question of the Day?
7 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 44 Views · 1 Like
Flag
📝 Reply
A tip: If you're unfamiliar with these regulations, just use your father's common sense to get the answer right.
▲
⟩⟩
SimpleSailor
💬 Re: Finally, back to work...
7 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 37 Views · 2 Likes
Flag
💬 Add Comment
Hi Jumpugly, good luck with your new work.
With the weight so much higher than expected, I'm curious to see how you'll resolve it, but I'm sure you'll find the right solution.
You've reminded me that I need to get back to work, too.
A bit of indolence and laziness have crept in; I need to overcome this post-holiday inertia.
With the weight so much higher than expected, I'm curious to see how you'll resolve it, but I'm sure you'll find the right solution.
You've reminded me that I need to get back to work, too.
A bit of indolence and laziness have crept in; I need to overcome this post-holiday inertia.
▲
⟩⟩
jumpugly
hermank
📝 Question of the Day?
8 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 41 Views · 0 Likes
Flag
📝 Reply
Yes Nick, you said it right, hahahaha.
▲
⟩⟩
No likes yet
This member will receive 1 point
for every like received
This member will receive 1 point
for every like received
📝 Question of the Day?
8 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 40 Views · 2 Likes
Flag
📝 Reply
EdW you took the words right out of my mouth (I don't know if that's the right expression), you read my mind and it's the same reasoning I did.
▲
⟩⟩
Steves-s
Nickthesteam
📝 Dragonflite Sails
9 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 38 Views · 2 Likes
Flag
📝 Reply
Ross gave excellent advice, a truly practical guide. It's clear he's faced these problems firsthand.
▲
⟩⟩
hermank
Ronald
Login To
Remove Ads
Remove Ads
📝 Question of the Day?
10 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 41 Views · 1 Like
Flag
📝 Reply
Phil, I've come to realize that these sorts of lapses in the counting system happen from time to time.
I've also had this happen in the past, where I've responded, but the box would be marked as "no reply."
Today you answered correctly (judging by the colored lines), but yesterday you didn't respond.
I've also had this happen in the past, where I've responded, but the box would be marked as "no reply."
Today you answered correctly (judging by the colored lines), but yesterday you didn't respond.
▲
⟩⟩
RossM
📝 Question of the Day?
11 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 47 Views · 2 Likes
Flag
📝 Reply
Thanks so much for the explanations (I also received them via PM), much appreciated.
I never would have figured it out on my own.
Scooby-Doo reminds me of a cartoon I watched as a kid.
I never would have figured it out on my own.
Scooby-Doo reminds me of a cartoon I watched as a kid.
▲
⟩⟩
Doogle
DWBrinkman
📝 Question of the Day?
12 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 40 Views · 2 Likes
Flag
📝 Reply
Hi Doogle, sorry, but what do you mean by Scooby Doo?
I don't understand what you mean.
Have a good day too.
I don't understand what you mean.
Have a good day too.
▲
⟩⟩
hermank
Doogle
📝 Question of the Day?
12 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 46 Views · 1 Like
Flag
📝 Reply
Excellent, Ross, this makes today's question more useful and informative for everyone. Thanks.
▲
⟩⟩
RossM
📝 HAPPY NEW YEAR
12 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 24 Views · 4 Likes
Flag
📝 Reply
The hand pump is awesome, Mike!
Is it cold in Rothenburg?
Is it cold in Rothenburg?
▲
⟩⟩
Aquaholic
hermank
jumpugly
Mike Stoney
💬 Re: New Moth MKII semi scale yacht
12 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 43 Views · 4 Likes
Flag
💬 Add Comment
Great! The next project will be 1:1 scale, awesome Jbkiwi!
▲
⟩⟩
jumpugly
jbkiwi
stevedownunder
hermank
📝 Question of the Day?
12 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 47 Views · 1 Like
Flag
📝 Reply
Great idea, Ross, well done.
If you overlay it with an arrow (you can use any free photo editor like Paint), it's even better.
Someone might say you clearly suggested the answer, and perhaps it would have been better to do it tomorrow, but now a lot of time has passed and almost everyone has responded, so it doesn't matter.
From now on, please don't make mistakes!
If you overlay it with an arrow (you can use any free photo editor like Paint), it's even better.
Someone might say you clearly suggested the answer, and perhaps it would have been better to do it tomorrow, but now a lot of time has passed and almost everyone has responded, so it doesn't matter.
From now on, please don't make mistakes!
▲
⟩⟩
RossM
📝 Question of the Day?
13 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 43 Views · 1 Like
Flag
📝 Reply
Great tools Dave.
▲
⟩⟩
DWBrinkman
📝 Question of the Day?
13 days ago by 🇮🇹 AlessandroSPQR ( Fleet Admiral)
Fleet Admiral)
 Fleet Admiral)
Fleet Admiral)✧ 43 Views · 2 Likes
Flag
📝 Reply
Today's question, after finding the correct terms in Italian, seemed simple enough.
Yet, there was one term among the four I couldn't find, or rather, I couldn't find any relevance to the naval field.
Eventually, I found it and understood what it was.
Of course, it wasn't the right answer because I had already identified the correct one, but I wanted to be sure.
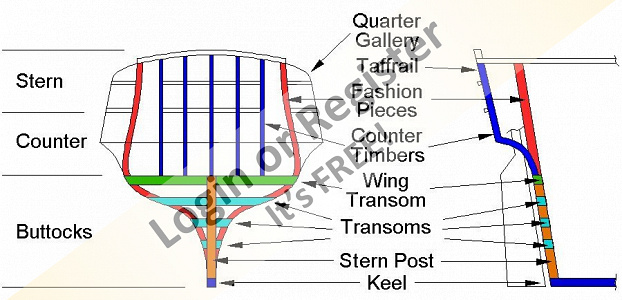
Yet, there was one term among the four I couldn't find, or rather, I couldn't find any relevance to the naval field.
Eventually, I found it and understood what it was.
Of course, it wasn't the right answer because I had already identified the correct one, but I wanted to be sure.

▲
⟩⟩
SimpleSailor
RossM





 Lieutenant Commander)
Lieutenant Commander)

 Chief Petty Officer 1st Class)
Chief Petty Officer 1st Class)

 Commander)
Commander)

 Leading Seaman)
Leading Seaman)

 Commodore)
Commodore)


 Captain)
Captain)


 Vice Admiral)
Vice Admiral)

 Rear Admiral)
Rear Admiral)












